你知道吗?在我们周围的世界里,有一种神奇的几何图形,它不仅有着独特的数学魅力,还在我们的生活中扮演着重要角色。这就是阿基米德螺旋线,一个由古希腊数学家阿基米德发现的神奇轨迹。今天,就让我带你一起探索这个充满魅力的几何世界吧!

阿基米德螺旋线,又称为等速螺线,这个名字本身就充满了速度与力量的感觉。它是由一个点匀速离开一个固定点,同时以固定的角速度绕该固定点转动而产生的轨迹。想象一个勇敢的点在旋转的同时,不断向外扩张,这不就是我们生活中不断追求进步、勇往直前的缩影吗?
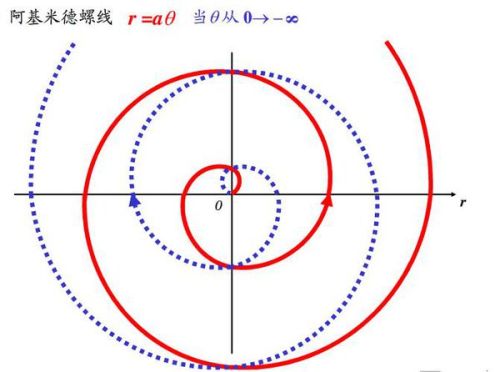
阿基米德螺旋线的数学表达式为:r = a bθ,其中,r表示点P到极点O的距离,a表示螺旋线的初始半径,b表示相邻两圈螺旋线之间的距离,θ表示点P与极轴的夹角。这个方程式简洁而优美,仿佛在诉说着一个关于成长与进步的故事。
阿基米德螺旋线具有许多独特的性质,其中最引人注目的是它的等距特性。这意味着,无论在螺旋线的任何位置,只要转过相同的角度,两角度间距离中心的距离都是一固定值。这种特性使得阿基米德螺旋线在许多领域都有广泛的应用。
阿基米德螺旋线不仅在数学领域有着重要的地位,还在我们的生活中扮演着重要角色。以下是一些阿基米德螺旋线的应用实例:
1. 灌溉系统:阿基米德螺旋线的等距特性使得它成为灌溉系统的理想选择。通过旋转的螺旋线,水可以均匀地分布到整个灌溉区域,提高灌溉效率。
2. 机床卡盘:在机床加工过程中,阿基米德螺旋线可以用来设计卡盘,确保工件在加工过程中的稳定性。
3. 无线电天线:阿基米德螺旋线被广泛应用于制造无线电天线。由于其对称性和具有相同螺旋角的多个线圈的耦合性,它被认为是一种非常有效的无线电天线形态。
4. 轮胎胎面纹路:阿基米德螺旋线被应用于轮胎胎面的纹路设计中,这种设计可以提供更好的排水能力和抓地力。
5. 建筑与生物学:阿基米德螺旋线在建筑设计和生物学领域也有所体现。例如,螺旋楼梯、摩天大楼的外观设计以及DNA的双螺旋结构等。
随着科技的不断发展,阿基米德螺旋线在各个领域的应用将会越来越广泛。相信在不久的将来,这个神奇的几何图形将会为我们的生活带来更多的惊喜。
阿基米德螺旋线是一个充满魅力的几何图形,它不仅有着独特的数学魅力,还在我们的生活中扮演着重要角色。让我们一起期待这个神奇的几何世界带给我们的更多精彩吧!